How I would allocate my portfolio in 2024 (a joke, sort of)

Photo by LJ on Pexels.com

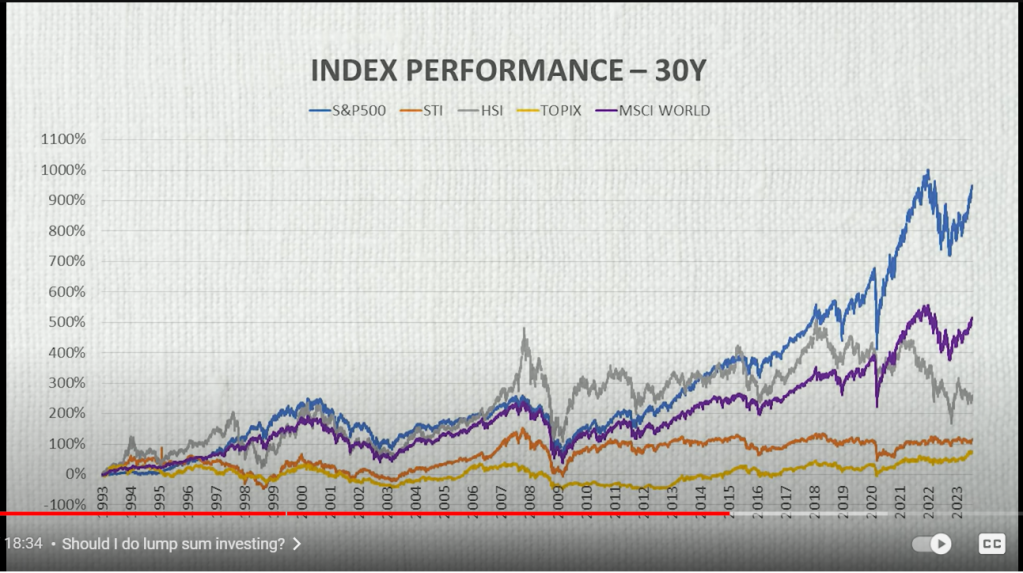
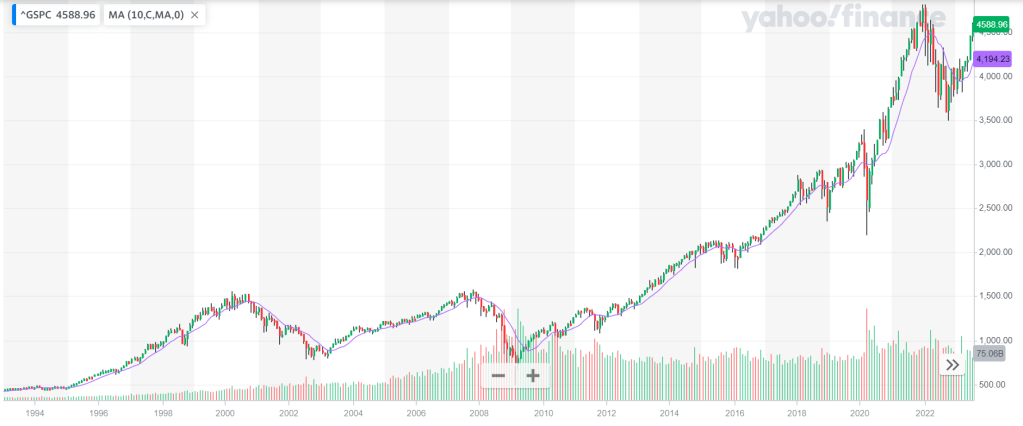
I’ve been seeing these sorts of posts on my feed and most of these posts are so badly written because they don’t consider any individual investor’s circumstances and/or no finance theory behind the allocation so I thought I’d ask Google’s Gemini Pro (GGP) to take a stab at it.

The rest of the post is the response from GGP.

What do y’all think of GGP’s take on asset allocation for 2024?

**Asset Allocation:**
* Stocks: 70%
* Bonds: 15%
* International Stocks: 10%
* Singapore Real Estate: 5%

**Index Funds and ETFs:**

* **Singapore Stocks:**
* **STI ETF (SGX: STI):** This ETF tracks the Straits Times Index, which represents the 30 largest and most liquid companies listed on the Singapore Exchange (SGX).
* **Nikko AM Singapore Dividend Leaders ETF (SGX: NDLV):
** This ETF invests in Singapore companies with a history of paying dividends.

* **International Stocks:**
* **Vanguard Total International Stock Index Fund (VXUS):
** This fund offers exposure to stocks from developed and emerging markets outside Singapore and the U.S.
* **iShares Core MSCI EAFE ETF (IEFA):
** This ETF provides exposure to developed markets outside Singapore and the U.S.

* **Bonds:**
* **ABF Singapore Bond Index Fund (SGX: A35):
** This ETF tracks the FTSE Singapore Bond Index, which represents the Singapore dollar-denominated bond market.
* **LionGlobal SGD Enhanced Duration Bond ETF (SGX: LDS):
** This ETF invests in Singapore government and corporate bonds with longer maturities.

* **Singapore Real Estate:**
* **Ascendas REIT (SGX: A17U):
** This REIT invests in a portfolio of industrial properties in Singapore.
* **CapitaLand Integrated Commercial Trust (SGX: C38U):
** This REIT invests in a portfolio of shopping malls, offices, and serviced residences in Singapore.

**Investment Strategy:**
* **Regular Contributions:
** * Consider setting up a recurring investment plan to contribute a fixed amount to your investment accounts each month. This strategy, known as dollar-cost averaging, can help reduce the impact of market volatility and potentially increase your returns over time.
* **Rebalance Annually:**
* Once a year, review your portfolio’s asset allocation and rebalance it if necessary. This means selling some assets that have performed well and buying more of those that have underperformed. Rebalancing helps maintain your desired asset allocation and risk level.

* **Stay Invested for the Long Term:**
* Remember that investing is a long-term game. Avoid making impulsive decisions based on short-term market fluctuations. Stay invested through market downturns, as history has shown that stocks tend to recover and reach new highs over the long term.

**Additional Considerations:**

* **Tax-Advantaged Accounts:**
* Consider investing in tax-advantaged accounts, such as the Supplementary Retirement Scheme (SRS) and the Central Provident Fund (CPF), if available. These accounts offer tax benefits that can help your investments grow faster.

* **Emergency Fund:**
* Before investing, make sure you have an emergency fund with 3-6 months of living expenses saved up. This fund can help you cover unexpected expenses without having to sell your investments. *

**Investment Goals:**
* Keep your investment goals in mind when making investment decisions. If you have a long-term goal, such as retirement, you may be able to tolerate more risk in your portfolio.

* **Risk Tolerance:**
* Assess your risk tolerance and invest accordingly. If you are uncomfortable with the potential for large swings in your portfolio’s value, you may want to allocate a larger portion of your portfolio to bonds and other less volatile investments.

**Disclaimer:** Investing involves risk. Past performance is not a guarantee of future results. The information provided is for general informational purposes only and should not be construed as investment advice. It is essential to consult with a qualified financial advisor before making any investment decisions.

**Note:** The investments mentioned above are just examples, and the specific funds or ETFs you choose may vary depending on your individual circumstances and investment goals. It is always a good idea to consult with a qualified financial advisor in Singapore who can provide personalized advice based on your unique situation.

Goodbye 2023

Photo by Eric Christian Capilador on Pexels.com

This year has been tiresome.

I’ve never been so overwhelmed and bored at the same time. I’ve been filled with both worry and hope, and the year has come and gone without major disaster in my life.

My heart goes out to those whose lives continue to be affected by the wars in Ukraine and the Gaza Strip and it’s a constant reminder of how lucky I am to live in a country where the biggest gripe in recent memory seems to be how Ya Kun has raised the price on their kaya toast set from S$4.80 to S$6.30 within a year.

Once I realise how peaceful life here is, it turned out my year had been good after all.

Portfolio

Alas, I wish I could say that my portfolio did wonders this year but if you were invested outside of the major indexes like I was, this year would have been very subpar in terms of returns.

Nevertheless, my portfolio^ has reached a new milestone because of my high savings rate and because I let the dividends compound. The negative sentiment surrounding interest rates staying higher for longer in September and October also provided a good opportunity to deploy a little more investments into REITs which were beaten down further although there has been quite a sharp rebound since November.

^(To be clear, my portfolio only includes cash set aside for investments and the market value of my money invested in equities, bonds, and other financial instruments. I DO NOT include the value of my share of the property used as a residence and the monies in my CPF. I track these numbers as part of my Net Worth but when I say “portfolio”, I’m referring to the value of my investments alone.)

For privacy reasons, I won’t report the actual amount in the portfolio. Let’s just say that it’s a six-figure portfolio which is not quite F- You money but it isn’t chump change either. Based on growth rates, the portfolio’s CAGR is around 23% over its lifetime of 15 years but much of this is due to the low starting base (a low five-figure sum) and subsequent stuffing of cash into the portfolio over that same period.

Yes, I’ve been saving a lot of money and the main reasons for that are: (1) I’ve worked in the government all my life, drawing a decent (but not obscene) salary that would put me around the 70-80th percentile of income earners in Singapore, (2) I have family (spouse included) that are pretty self-sufficient although I have been giving a token sum to my parents all these years, and (3) I don’t have kids.

I hope the above reasons are clear to demonstrate that not everyone in Singapore will be able to get to where I am in 15 years but I estimate that even without the second and third reasons, my portfolio would still be six figures but half or a third of what it currently is. I also hope that this doesn’t come across like I’m bragging because I’m not. In fact, if I were more disciplined with my investments, I reckon my portfolio would be seven figures or at least it would be very much closer to that milestone.

Money, Money, Money

In terms of net worth, it has continued to climb in line with the portfolio and no thanks to the forced CPF contributions required by the government. The property market in Singapore has continued to remain resilient despite higher interest rates and the new models that the Government has introduced to the BTO market. Nevertheless, I don’t track the market value of my property and value it at cost.

The biggest epiphany I’ve had this year is that many people in Singapore are probably not going to do well in retirement because they have little to no assets (besides their primary residence) that can help fight against inflation.

This year is probably the year where the mental budget for the cost of dining out in Singapore has reached a minimum of S$10 per meal. I remember visiting either the UK or Australia as a kid and thinking that dining out in those countries was so expensive because the average meal cost between 10-15 units of their currency.

Ladies and Gentlemen, I think this year will be the year where we can say that Singapore has reached that mark. If you dine out at any one of the newer hawker centres or coffeeshops, you’ll see that many of the mains are priced at around S$6-8. Once you add a cold drink, that’s easily close to S$10. If you go beyond the hawker centres and coffeeshops, it’s going to be very difficult to stay under S$10 per meal.

The wonderful thing about high(er) interest rates this year is that many risk-averse individuals learned about the joys of investing in T-bills. While that helped with the inflation situation a little, it didn’t actually help people get wealthier. If you think of someone running on a super long treadmill, T-bills just prevented someone from falling off the treadmill, it didn’t necessarily help them get ahead of the pack.

Invest in real assets, my friend.

This year really underscored the importance of owning real assets – businesses, real estate, or anything that allows for increasing prices over time.

While the principle is simple, the difficulty is in identifying which assets to own. Furthermore, the assets have to be purchased at a reasonable price, or the rate of return may not be sufficient to provide a return high enough to beat inflation.

Despite it being a difficult task, I don’t think one should avoid it unless you have a huge enough source of capital such that mediocre returns will still provide enough dollar returns for any current and future expenses.

Ok, that’s all I have to say. I know I haven’t been blogging much but that’s life.

Best Things I’ve Read All Week (3 Sep ’23)

Singapore gets a new president this week. It’s the first time since the contest of the four Tans that we’re getting to vote so the results could be a signal of the reaction to the controversy over the changes that made the previous Presidential Election a reserved election which resulted in no contest. It could also be a result of the recent issues that have plagued the ruling party.

In other news, markets seem to have gotten over flagging Chinese economic growth and Fed Chair Jerome Powell’s remarks at Jackson Hole don’t seem to have soured the mood despite his comments on rates likely being higher for longer. Markets have resumed the upward momentum following the slight tumble in August.

Finally, the One Piece Live Action series has been released on Netflix! I didn’t have high hopes for it because of how bad live-action series usually turn out but I have to say that the series has turned out much better than expected. I’m only 4 episodes in but it’s been good so far.

Photo by Mikes Photos on Pexels.com

The Scam in the Arena
(newcomer.co)

I’ve said it before. Chamath is a shameless self-promoter and not a great investor.

Is a degree worth it? (Today Online)
‘What they told me kind of shocked me’: Singaporean compares fresh-grad salaries with Taiwan’s (Asiaone)

There’s also the CNA documentary on YouTube that profiles how much young Taiwanese are earning and how they’re living in Taipei. It’s crazy how young graduates there find themselves spending a large chunk of their wages on stuff like rent and food. No wonder their birthrates are even lower than ours.

All these tie into the question posed in the first article and it is a question of particular relevance to young people today. It’s also a question that many of my former students struggled with as polytechnic students because in practice, polytechnic education is supposed to prepare them for work but they face parental and personal expectations to further their studies.

I’m of the camp that one needs to be very clear on whether the job one wants to do requires much formal study or not. I’ve seen far too many people with degrees end up in jobs that don’t require them to apply what they’ve studied in university. Then, there’s also the question of whether it’s possible to pick some knowledge and skills outside of school. With online learning on demand, it’s becoming increasingly so.

15 Ideas, Frameworks, and Lessons from 15 Years
(Newfound Research)

Great points from Corey Hoffstein.

My best learning point from going down the rabbit hole into his work is the idea of Rebalancing Timing Luck. I’ll never look at backtests in the same way again.

Best Things I’ve Read All Week (20 Aug ’23)

It’s official. Singapore goes to the polls to elect a President on 1 Sep 2023.
In other news, markets have been coming down over the last couple of weeks. Bitcoin has also fallen off a cliff in the span of 3 days.

Photo by Mikes Photos on Pexels.com

$1b anti-money laundering raid in Singapore: Who are the 10 people charged? (Asiaone)
$1b money laundering case: 11 more properties linked to suspects (Asiaone)

I think what amazed me was the sheer number of properties in Singapore linked to this case. Also, given the information needed to even move money here and complete the transactions, wouldn’t all this have been flagged a lot sooner?

My tongue-in-cheek personal conspiracy theory is that the authorities identified the gang earlier on but allowed for the gang to complete moving a sizable sum here before nabbing them. The reason? So that the assets get sold once (benefitting sellers) and then get seized so that they can be sold again to generate another round of taxes collected.

If this were true, that’s some serious 4D chess that the authorities just played.

It Takes Nearly 3 Decades And Half A Million Bucks For An Average Singaporean To Feel Financially Free; 2023 Singlife Study Finds (Yahoo Finance)

$500K SGD seems rather low to me. I’m not sure what the survey asked to get the number but I expected the number to be closer to a million.

Nvidia circa 2023, Cisco circa 2000
(FT.com)

Hidden behind a paywall but greats charts showing the similarities between Nvidia’s shares today and Cisco’s back during the dot-com boom (and subsequent bust).

Best Things I’ve Read All Week (13 Aug ’23)

Photo by Mikes Photos on Pexels.com

STI ETF Dollar Cost Averaging Generated 5% CAGR from Dec 2019 to Jul 2023
(SGX.com)

I’m not sharing this link to state how great DCA is. Rather, I’m sharing this as a reminder of how DCA-ing in non-trending (or down-trending markets) makes little difference to your portfolio. And this is how you calculate returns, not like some folks who only look at price returns. Of course, the biggest downside to DCA vs. lump-sum will be any fixed transaction costs. That will probably make all the difference for retail investors who only invest small amounts at each go.

5 BIG LESSONS POPULAR PERSONAL FINANCE ADVICE GETS WRONG
(Gen Y Planning)

Basic but useful.

A Few Stories About Big Decisions
(Collab Fund)

Morgan Housel is such a great writer.

The Morris Chang story is funny. An additional $1 a month.

Finfluencers can’t finance: The Fifth Person edition

In a previous post, I wrote about how one Singaporean personal finance/investing personality got it totally wrong about Dollar-Cost Averaging.

Recently, another local outfit that purports to teach people about investing went into the same topic and came to terrible conclusions on the back of bad analysis.

The Fifth Person created a video titled “Lump Sum Vs Dollar-Cost Averaging – Which Is Better? Truth Revealed…” which came to several dubious conclusions.

Around the 11:55 mark, one of the presenters makes the claim that Dollar-Cost Averaging (DCA) or Lump-sum investing won’t work if you have markets that went nowhere and he cited the example of the Japanese stock market and presented this travesty of a chart.

Source: The Fifth Person YouTube channel

The biggest problem I have with this chart is the fact that these are price returns. Although the chart doesn’t explicitly say that these are price returns, I went to Yahoo Finance and pulled up the chart of the S&P500 over the same period, and lo and behold, it is indeed a price chart.

(note: you can tell it’s the same returns from the same of the curve or if you want to do your own due diligence, what I did was look at the returns from 1 Jan 1993 to 31 Jul 2023 which comes up to 953.21% which is roughly what’s indicated in the chart above.)

Source: Yahoo Finance

Dividends are part of returns

So why is this a problem? Well, finance 101 tells us that the source of equity returns can be divided into two parts – returns from income and returns from multiples expansion.

When you look at price returns, it only accounts for the returns due to increased earnings (which are only one part of earnings) and multiples expansion. A large part of returns from income comes in the form of dividends or in more recent times, share buybacks.

Finance theory tells us that when a company makes money and pays dividends, it reduces earnings left to reinvest in the business and therefore isn’t reflected in the price of the stock as those returns have already been realised (or consumed, if you like) by the shareholder and therefore should not be reflected in the price.

And the data proves it.

Total returns are often higher than Price returns and studies have been done to show that dividends provide anywhere from 30-50% of returns to an investor. For example, see this white paper by Hartford Funds.

Back to DCA

So back to the topic at hand.

In fact, logic would dictate that DCA would do better than lump-sum when markets are trending down or going nowhere since you keep accumulating additional shares at lower prices. In the case of the Nikkei, others have already done the work.

This post by A Frugal Doctor shows that an investor who DCA-ed $833 per month from Dec 1989 (the height of the Nikkei bubble) to Dec 2019 would have a portfolio of $617,545 while an investor who started with a lump-sum of $300,000 would have seen their portfolio shrink to $272,318 within the same period.

(Note: For those that prefer rates of return, DCA-ing into the Nikkei would have given a Money-Weighted Rate of Return of 4.22% p.a.. In a world where interest rates were zero or even negative, I think many Japanese would have been happy with 4.22% p.a..)

I’m not sure what those guys from The Fifth Investor consider “doesn’t work” but a result that is 227% better than the other option is a result that works for me.

Final Thoughts

I’m not saying that DCA is the best strategy out there or that it provides superior returns to lump-sum investing. I’m just saying that you have to know when it works and when it doesn’t. You also have to know how to measure returns accurately otherwise you’ll come to very wrong conclusions.

If you’re a beginning investor, you really need to be aware of the kind of advice that many finance YouTubers are peddling. Very often, these guys know a little to get started but not enough to get it right.

They’re also incentivised to get views so that they can make money from ads or through their affiliate links so they’ll do stuff like put a very click-baity title to get you to watch their videos. Oh, and those that sell a course for a few hundred bucks are the worse because all they teach are stuff cobbled together from the internet which you could have done for free.

All it takes is some time and effort.

Best Things I’ve Read All Week (6 Aug ’23)

The weekend before Singapore’s National Day!

Singapore turns 58 and having been born in Singapore and lived here all my life, I am proud to say that I have no regrets. While Singapore’s not perfect, I think it’s one of the few countries in the world where it’s safe even for a woman to go home alone at night. The public transportation here is also amazing – it’s affordable, convenient, and (mostly) reliable. Government spending is also not profligate, which is reflected in our fairly stable and strong currency. Lastly, while the ingredients are not the freshest because almost all of it has to be imported, the food is still amazing.

Happy National Day, Singapore!

Photo by Mikes Photos on Pexels.com

THE ROBO-ADVISOR CHOICE PARADOX
(cheerful.egg)

I didn’t realise that Endowus now has nearly 190 funds available for retail investors to choose from. That’s a ridiculous number of funds and really shows that they’ve lost the plot. In my course of work, I’ve met many fund houses trying to pitch different products and honestly, after hearing so many different pitches, they all sound the same.

Recently, I’ve been talking to many fund managers about ESG investing and it turns out that all of them pretty much tell me the same thing – it depends on what you want.

Need a product that excludes contentious sectors? No problem.
Need one that focuses on aligning the fund’s investments with the Paris Agreement? Sure, we have it.

And therein lies the rub. Fund managers just want your money. They don’t really care whether ESG makes sense as an investment or whether the way they implement ESG in investments makes sense; they’ll come up with products that they think clients will buy and the reason they have so many different types of products is because they have as many different types of clients.

If you ask me, a great fund is like a sushi master. A great sushi master focuses on making great sushi. If you don’t like sushi, that’s your right. Just go eat something else. The sushi master doesn’t care about your business, he just wants to be good at what he does.

Safe Withdrawal Rates Reading

The Problem with the 4% Rule (and Why You Could Retire Even Sooner) (madfientist)

The Problem With FIREing At 4% And The Need For Flexible Spending Rules (kitces.com)

Decision Rules and Maximum Initial Withdrawal Rates
(Journal of Financial Planning)

Kyith from Investment Moats did a great in-depth video on the 4% rule which led me down this rabbit hole because I’ve been aware of the other research surrounding safe withdrawal rates.

The first link provides a great point on a strategy that adjusts withdrawals based on returns in the stock markets (which impact portfolio values) and incorporates the idea that not all spending is necessary. If one is willing to adjust withdrawals for discretionary spending when times are bad, that greatly mitigates the sequence of return risk and therefore extends the longevity of the portfolio.

The second link provides an overview of safe withdrawal strategies alternative to the 4% rule.

The third link is to a paper by Guyton and Klinger which, using monte carlo simulation, provides insight into how different withdrawal rules affect a portfolio over a 30- and 40-year period. The findings of when portfolios are likely to run out of money also point to the usefulness of having a flexible withdrawal strategy (such as the strategy outlined in the first link). Very interesting paper.

Best Things I’ve Read All Week (30 Jul ’23)

The Fed hiked once more but it seems that at this point, the market doesn’t really care. As long as inflation heads in the direction its been going and the economic data supports a soft landing, things are going to be just fine for markets.

Photo by Mikes Photos on Pexels.com

Underperforming Your Own Assets
(The Big Picture)

Two lessons from this post – one, many people make the error of omitting dividends when calculating stock returns, and two, many people underperform total returns due to their behaviour.

When Hindsight Becomes Foresight: Replicating Investment Performance
(Enterprising Investor)

What a great post! The authors use two approaches to determine if a fund actually does what it claims to do or whether its performance can be replicated – either by market factors or a combination of holding the S&P500 and cash.

The tool highlighted in the post is pretty fun to play around with.

The Comfort Crisis
(Mr Money Mustache)

The cause of all our #firstworldproblems is the comfort it brings.

This post hit me like a brick because it’s so right. It’s not like I don’t know this but most of the time, I’m just blissfully unaware of how much of a problem it is.

Commercial Real Estate Is in Trouble, but Not for the Reason You Think
(Morningstar)

Really good article on the commericial real estate market in the US. The highlight of the article is that many investors don’t have a huge segment of the commercial real estate market, Multifamily homes, on their radar. This segment is set to see a huge number of loans get renewed this October which means higher rates and in turn, higher rents. However, the silver lining is that many of the loans are packaged in Commercial Mortgage Backed Securities (CMBS) and those that are agency-backed have a government agency backing it which, in theory, limits any chance of default.

Best Things I’ve Read All Week (23 Jul ’23)

What a week for Singapore politics! Having said that, it’s all basically noise as far as I’m concerned.

Photo by Mikes Photos on Pexels.com

Crafting an Ideal Passive Investment Portfolio for Your Life Goals
(Investment Moats)

Kyith from Investment Moats has done a commendable video that gives an overview of asset allocation and the kind of returns one could expect from a well-diversified portfolio built using passively-managed ETFs. A good primer if you’re completely new to investing^.

^When I say new, I really mean the kind of person that has never heard of diversification, index funds, and the like. If you’ve been purely investing in single-name stocks without regard to the portfolio level effects, you’re new.

The Extreme Cost of Active Management
(wealthmanagement.com)

A new study by Moshe Levy finds that when measured by Sharpe Ratios, most U.S. active equity funds (92.1%) underperformed a passive index. This study also finds little correlation between fund size and performance, and performance in the first half (Apr 2011 – March 2016) and the second half (Apr 2016-March 2021) of the period surveyed.

Yipes.

How to Get Rich in the Markets
(The Big Picture)

Barry Ritholtz provides his take on the various methods to get rich in the markets and the likelihood of each approach. No surprises here.

Best Things I’ve Read All Week (16 Jul ’23)

What a week in Singapore and the markets.

In Singapore, almost everything that anyone wanted to talk about this week was the high-profile investigation into an alleged corruption case linking Singapore’s Minister of Transport and a Malaysian billionaire based in Singapore.

As I read some of the alleged reasons for the probe, I can’t help but think that if true, it is what some would call the cost of doing business in other countries. In Singapore, we just don’t take this kind of stuff too lightly.

As for markets, investors are bulls again following the lower-than-expected CPI report in the US. The icing on the cake was the resignation of Bullard, one of the Fed members who is a notable hawk. Sadly, this means that valuations in US markets are getting more expensive.

Despite the higher valuations and turn in optimism, my gut feeling is that it’s too soon to turn bearish. Markets may climb higher for a while before the bears get to see their day.

Photo by Mikes Photos on Pexels.com

Against Cassandras: The government debt ‘bomb’
(Klement on Investing)

Joachim Klement provides a good argument on why those worried about Government Debt are likely to be wrong. Here is his summary of the entire argument:

Central banks have and in my view will continue to monetise government debt to keep long-term bond yields low if they have to. People who are afraid that this may create runaway inflation have to explain why this was not the case in Japan over the last three decades. The ageing demographics in the US and Western Europe even help governments in keeping demand for their bonds high and reduce the need for central bank intervention. And in the US, there is additional support from the fact that the US Dollar is the world’s reserve currency and foreign investors have to hold US Treasuries, whether they like it or not.

Gig workers ‘most financially stretched’ group in Singapore; spending exceeds income: DBS study
(ChannelNewsAsia)

Do we really need a study to tell us that the groups of people most vulnerable to inflation and rising interest rates are gig workers, boomers, and those with low income?

South Korea’s archaic rental system is costing people their life savings
(The Business Times)

I first read the full article on Bloomberg. It’s really interesting that a rental system like this exists because it is just so different from other residential rental markets around the world. Here’s a description of the system:

Under a system that’s unique to South Korea, landlords collect a deposit called jeonse that’s equal to anywhere from 50 per cent to 90 per cent of a property’s value at the start of the lease period, which typically runs for two years. Tenants usually pay no rent for the duration, while the property owner profits by investing the funds, often to buy or build more apartments. Landlords are contractually obligated to refund the deposit at the end of the lease term.

And this is how the scheme has endured and why it’s finally unravelling:

What’s essentially a government-sanctioned pyramid scheme – in which landlords pay back the deposits of tenants whose leases are expiring with funds obtained from new renters – worked relatively smoothly when property prices in the country’s major cities were climbing. But that decades-long trend was thrown into reverse when the Bank of Korea began aggressively raising interest rates in 2021 to tame inflation.

I’m just amazed that no one packaged these loans into securities and tried to offload the risk to retail investors when times were good. Imagine you owning the liability to pay your neighbour’s jeonse and your neighbour owning yours.

Who would have your back, a Skrull or a commissioned FA?
(Growing your tree of prosperity)

Why it makes perfect sense that real estate/insurance agents and FAs are braggy
(The Woke Salaryman)

Sunday double feature on Financial Advisors in Singapore. As usual, Christopher Ng writes well and The Woke Salaryman tries to put across a point of view that isn’t very controversial or antagonistic. I don’t disagree with their points.

In fact, I agree that the system as it is designed right now, doesn’t benefit the customer.